백준 16748 Colorful Tree

 16748번: Colorful Tree (acmicpc.net)




오일러 투어 테크닉을 이용하여, 트리를 선형으로 핀다음, Map을 통해, 한 서브 트리가 가지는 특정 색깔의 갯수를 세그먼트 트리를 통해 O(log N)에 찾을 수 있다.

자바는 시간이 빠듯하여, 바텀업으로 하는 것을 추천한다.
O(N(log N)^2)의 상수를 최대한 줄여야 한다. 여유? 그건 C++

어떤 하나의 색깔이 추가 될 때, 트리를 최적화 하게 만들어 둔다고 했을 때, 추가 하는 색깔의 위치는, 그 전 색깔을 통해 만들어진 최적화 트리를 통해 만들어진 LCA의 서브 트리 아래에 종속되어 있거나, 서브트리에 속하지 않는다.

1. 서브트리 아래에 종속 되어 있을 때

1. 최적화 된 트리 안에 색을 추가하는 경우는 트리의 크기에 변화를 주지 않는다.

2. 최적화 된 트리 바깥에 색을 추가하는 경우는, 서브트리에서 색을 발견 할 때까지 거슬러 올라가, 거리를 더해준다.

2. 서브트리 바깥에 있을 때

1. 특정 노드의 서브트리 안에 색을 발견 할 때 까지 거슬러 올라가 거리를 더해준다.

 그 지점이 색의 LCA를 서브트리로 가지고 있는 다면, LCA와의 거리도 더해준다.


특정 색깔의 LCA는 깊이가 가장 높은 노드부터, 루트 노드까지의 경로 선상에 존재하게 된다.

색깔의 LCA는 그 경로 선상에서 서브 트리가 특정 색깔을 모두 가지고 있는 노드 중, 제일 하위 노드이다. 이런 색깔의 LCA는 루트와 특정 색깔의 최하위 노드의 경로 선상에서 파라매트릭 서치를 하면 된다. 이 경우 파라매트릭을 하며, 세그먼트 트리 쿼리를 날리므로, O(log N) ^ 2 이다.

색을 발견 할 때 까지 거슬러 올라 가는 것도, 루트와의 경로에서, 파라매트릭 서치를 하며, 세그먼트 트리 쿼리를 날리면 된다.


색깔에 대한 트리의 크기 응답에는 O(1)

색깔을 바꾸는 데에는 O(log N ^ 2 )가 소요된다.


색깔을 없애는 방법은 그 위치에 대한 색깔정보를 없애 버리고, 새롭게 추가하려는 시도를 한다. 그 때, 업데이트로 이루어지는 추가되는 트리의 크기가 색깔 제거로 인해 없어져 버리는 트리의 크기와 같다.


색깔의 최하위 노드는 우선순위 큐를 이용하여, 관리한다.

최하위 노드 자체를 저장하는데, 우선순위는 깊이가 높은 순이다.

특정 컬러의 최하위 노드를 저장하는 우선순위 큐에 대해, 최대 100000의 추가 쿼리를 날리게 되고, 컬러에 저장 된 노드의 색깔이 현재 색깔이랑 맞지 않는다면 제거한다. 그럼 최대 50000의 제거를 하게 되고, 대충 O(N log N)이 걸리게 된다.


자세한 증명은 여백이 부족해 생략하도록 하겠다.


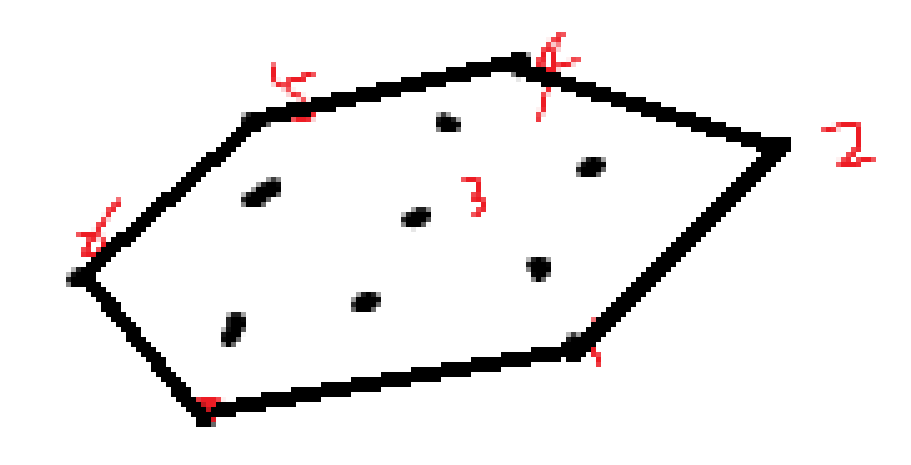
트리는 한점을 기준으로 한방향으로 쫘악 펼치면, 분기점이 있는 배열로 볼 수 있다.

숲을 보기보단 나무를 보는 느낌으로 접근하면 쉽게 트리에서 파라매트릭을 할 수 있다.


또한 LCA를 구하는 시간을 줄이기 위해, HLD나, 희소배열을 사용 할 수 있다.

세그먼트 트리 또한 활용해야 한다.


총 시간은 O(N (log N) ^ 2 ) 이 나오게 된다.



이 문제가 왤논이라면서 추천한 친구란놈은 무릎을 꿇도록 하자.

댓글

댓글 쓰기

이 블로그의 인기 게시물

SW - IT 충남대 콘테스트 문제 풀이 + 후기

이미지
 나는, 22학년도 충남대 컴융 신입생이다. 초반엔 극히, 평범한 학생이었고, 술마시고 게임만 하는 페인의 삶을 살았다.  TMI.1 지금은 PS페인이다. TMI.2 FPS만 극한으로 파던 사람이다. 4월 쯤인가? 학교 코딩 테스트에서, 간단한 별 찍기 문제가 나왔다. 그 문제에서, 너무 괴로웠고, 쉽게 하는 친구들을 보며, 자괴감이 들었다. 그 후, 만난 컴융 친구들 중, 배인수 (사인은 PS로 인한 혈압사)라는 친구가 백준을 하고 있고, 실버를 찍은 것을 보여주었다. 별 찍기 같은 문제들을 잘 풀고 싶은 마음도 있었고, 친구가 실버를 찍은 것을 보니 나도 백준을 하고 싶었고, 기숙사에 들어가자 마자, 백준에 들어가 문제를 미친듯이 풀기 시작했다. 이게 PS페인의 시작이었다.. 그리고 5개월 후... SW - IT 콘테스트가 열렸다. 나는 그래도 나름 고인물이 되어있고, 개같이 신청을 넣었다. 그리고 본 대회에서 9솔을 했다. 솔직히, 시간이 있으면 충분히 다 풀지만, 대회라서 긴장하고 있었고, 시간도 촉박 하다는 압박감, 그리고 초반에 실수를 너무 많이 해서, 아래서 올라오는 순위에도 정신이 너무 팔려 있었다. 실제로 대회에서, 했던 생각을 바탕으로, 간단한 문제 해설과, 문제 리뷰를 해보겠다. 진짜 아주 간단하게 해설을 썻으니, 한번 쓱 보고 문제를 푸는 것을 추천한다. 혹여나, 대회에서 기대 이하의 성과를 이룬 사람들은, 노력해서, 다음에 목표한 성과를 이루길 기원한다!! Division 1 내용만 다룬다. 2022 충남대학교 SW-IT Contest - Division 1 (acmicpc.net) 25628번: 햄버거 만들기 (acmicpc.net) min(빵 / 2, 패티) 가 정답이다. (정수 연산이다) 실제로 대회에서도, 여기까지 생각하고, 아무 생각없이 제출하고 다음문제로 넘어갔다. 25629번: 홀짝 수열 (acmicpc.net) 홀수는 홀수 칸에, 짝수는 짝수 칸에 있어야 한다.  홀수의 개수와, 짝수의 개수, 총...
자세한 내용 보기

볼록 껍질 알고리즘

이미지
플레티넘 이상의 문제에서 그리디 알고리즘이나 애드혹을 제외한 알고리즘들은 알고리즘을 구현하는 방법을 알고 있어도, 그 구현 자체와 개념 이해에 난이도가 붙는 방식이다. 즉 알고리즘을 알고 있을 때, 난이도가 플레티넘이라는 것이다. 플레티넘 이상 알고리즘 태그가 붙은 문제는 공부를 해야 풀 수 있다. 혼자서 푼다면, 대학원 가는 것을 추천한다. 그중 플레문제를 풀고 싶은 당신께 볼록껍질 알고리즘에 대해 소개해보자 한다. 정확히는 Graham Scan 알고리즘이다. 볼록 껍질 알고리즘이란, 좌표평면 상에 점의 집합이 구해졌을 때, 바깥 쪽 점들을 구하는 알고리즘이다. 이와 같이 나머지 점이 다 안쪽에 있는 다각형을 만드는 것이다. 내가 여기서 쓴 알고리즘은 꼭짓점을 구하는 알고리즘이다. 이해도가 높다면 개량하여, 모든 점을 구해보는 것도 시도해보는 것을 추천한다. class Point { int x, y; Point ( int x, int y) { this .x = x; this .y = y; } } 간단하게 CCW 를 구현 하여 보겠다. public static int CCW (Point a, Point b, Point c) { int g = (c.x - a.x) * (b.y - a.y) - (b.x - a.x) * (c.y - a.y); return Integer. compare (g, 0 ) ; } 반시계 일때 -1, 시계 일때 1, 평행할 때 0 을 리턴한다. 점들을 정렬하여, 맨 왼쪽 아래 점을 찾자. 그 점(central)은 볼록다각형에 무조건 포함된다. 정렬을 해보겠다. Arrays.sort(points, new Comparator<Point>() { @Override public int compare (Point o1, Point o...
자세한 내용 보기