볼록 껍질 알고리즘
플레티넘 이상의 문제에서 그리디 알고리즘이나 애드혹을 제외한 알고리즘들은 알고리즘을 구현하는 방법을 알고 있어도, 그 구현 자체와 개념 이해에 난이도가 붙는 방식이다.
즉 알고리즘을 알고 있을 때, 난이도가 플레티넘이라는 것이다.
플레티넘 이상 알고리즘 태그가 붙은 문제는 공부를 해야 풀 수 있다. 혼자서 푼다면, 대학원 가는 것을 추천한다.
그중 플레문제를 풀고 싶은 당신께 볼록껍질 알고리즘에 대해 소개해보자 한다.
정확히는 Graham Scan 알고리즘이다.
볼록 껍질 알고리즘이란,
좌표평면 상에 점의 집합이 구해졌을 때, 바깥 쪽 점들을 구하는 알고리즘이다.
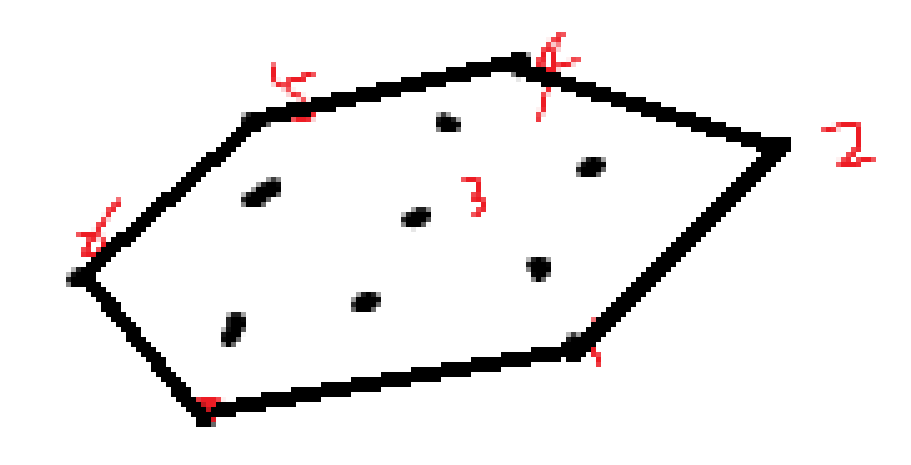
이와 같이 나머지 점이 다 안쪽에 있는 다각형을 만드는 것이다.
내가 여기서 쓴 알고리즘은 꼭짓점을 구하는 알고리즘이다.
이해도가 높다면 개량하여, 모든 점을 구해보는 것도 시도해보는 것을 추천한다.
class Point {
int x, y;
Point (int x, int y) {
this.x = x;
this.y = y;
}
}
간단하게 CCW 를 구현 하여 보겠다.
public static int CCW (Point a, Point b, Point c) {
int g = (c.x - a.x) * (b.y - a.y) - (b.x - a.x) * (c.y - a.y);
return Integer.compare(g, 0);
}
반시계 일때 -1, 시계 일때 1, 평행할 때 0 을 리턴한다.
점들을 정렬하여, 맨 왼쪽 아래 점을 찾자. 그 점(central)은 볼록다각형에 무조건 포함된다.
정렬을 해보겠다.
Arrays.sort(points, new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
if (o1.y == o2.y) return Integer.compare(o1.x, o2.x);
return Integer.compare(o1.y, o2.y);
}
});
Comparator 를 모른다면, 이 문제를 풀 수 없다.
풀 수 없다.
이 문제를 풀고 싶지만, Comparator가 뭔지 모른다면,
https://www.acmicpc.net/problem/1181
이문제를 Comparator를 이용하여 풀고 오면 된다.
자 그럼
기준점을 찾아 놓고, 배열에서 제거한다.
바깥쪽 점들을 찾을 건데, 점을 반시계 방향순으로 탐색 할 것이다.
그러니, 그 점(central)을 기준으로, 모든 점을 반시계 방향으로 정렬을 시도 하자!
al.sort(new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
return CCW(central, o1, o2);
}
});
어렵다고 느낄 수 있지만, 극복해야 한다.
ccw를 이용해 그 점의 상대적인 각도를 알 수 있다. o1, o2가 반시계 관계라면, central 에서 반시계로 돌릴 때, o1을 먼저 검사하게 되는 것이다.
6시 방향부터, 반시계로 돌면서 central을 기준으로 탐색을 시작할 수 있게 되었다.
Stack<Point> s = new Stack<>();
s.push(central);
for (int i=0;i<al.size();i++) {
s.push(al.get(i));
while(s.size()>2) {
Point c = s.pop(), b = s.pop(), a = s.peek();
int ccw = CCW(a, b, c);
// ccw 가 반시계 일 때 -1을 리턴한다.
if (ccw < 0) {
s.push(b);
s.push(c);
break;
}
//ccw가 1이나 0 을리턴하여, a -> b -> c 순서로 시계방향임이 입증되었다. 가운데 b점을 넣지 않음으로써, 빼게 된다.
s.push(c);
}
}
Point b = s.pop();
if (CCW(s.peek(), b, central) < 0)
s.push(b);
이제 스택에 넣어주면서 반시계로 탐색을 하는데, 시계방향으로 향하게 된다면, 반시계가 될 때까지, 스택에서 계속 제거해주면서 해주면 된다.
이해하는 것 자체가 플레티넘인 것이다. 이런 기하학적 발상을 코드로 이해한다는 건 어려운게 맞다.

그림을 보면 2번 3번 4번을 순서대로 연결 하면, 볼록한게 아니라, 들어가 버리게 된다...
들어가는 것 자체가 2, 3, 4를 CCW 하게되면, 시계방향이 나오는 것이다.
그러니 3번을 제거하고 4번을 담은다음 계속 검사를 하는 것이다.
근데 왜 stack이 2 이상일 때, 조건이 맞을 때까지 검사를 하는 것일까?
이러한 점의 집합이 있다고 해보자. 여기서 convex hull (볼록 껍질 ) 볼록 다각형을 이루는 꼭짓점을 찾을 것이다.
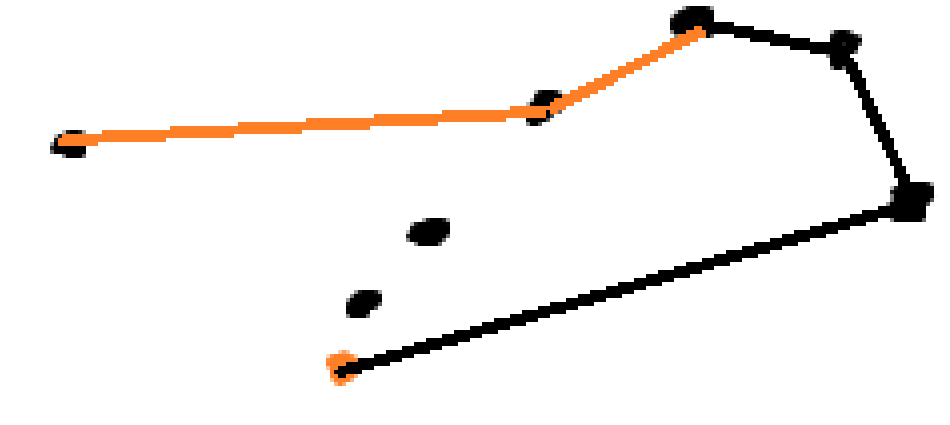
어찌 잘 진행하여, 이 상황 까지 왔다.
왼쪽 위 점을 연결 시도 해보자.
시계방향이다. 가운데 점을 빼고 다시 검사 한다.
또 시계 방향이다.
또 또 시계 방향이다.
드디어 반시계를 찾았다. 그럼 이제 검사 하느라 빼놧던것을 다시 다 넣고, 다시 진행하자.
어? 그런데 검사가 끝났다. 마지막 시작점과의 관계도 체크해준다.
이 개념을 이해하여, 코드를 보며 이해하도록 해보자.
마지막에 b를 다시 뺏다가 넣는것은, 이 b라는 점이 시작점 central과 연결 되었을 때, 볼록한지 체크해야 하기 때문이다.
이렇게 스택에 볼록다각형을 이루는 꼭짓점들을 다 담았다.
int 형으로 안된다면, long 형으로 변환하여, 오버플로우를 예방하도록 하자. 오버플로우가 나는 순간 관계가 변하게 된다. 주의하자
사실 이 알고리즘은 O(N log N) 이다.
정렬에서 시간을 잡아 먹기 때문이다. ㅎ
이 알고리즘을 활용해, 점의 집합에서, 가장 먼 두 점을 구할 수도 있고, 아무튼 요긴하게 쓰인다.
자바로 할 때, Arraylist를 쓰는 것을 권장한다.
자 이제 플레티넘 문제를 풀러가자







댓글
댓글 쓰기